Ask AI: what is the equation in slope intercept that passes \left(-4,2\right) and \left(12,6\right)

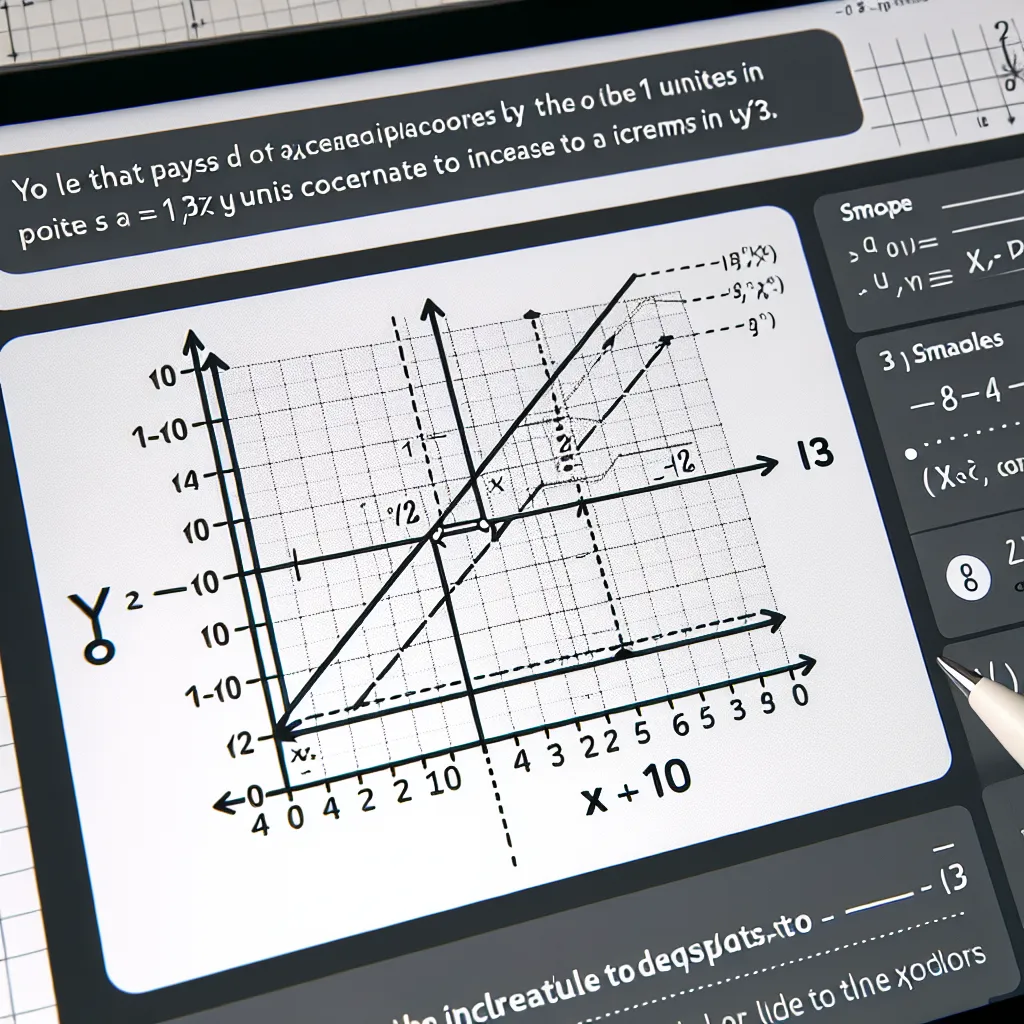
To find the slope-intercept form of the equation of the line passing through the points \((-4, 2)\) and \((12, 6)\), we start with the formula for the slope of a line, which is: \[ m = \frac{y_2 - y_1}{x_2 - x_1} \] Given the points \((-4, 2)\) and \((12, 6)\), we designate the coordinates as follows: \((x_1, y_1) = (-4, 2)\) \((x_2, y_2) = (12, 6)\) Substitute these values into the slope formula: \[ m = \frac{6 - 2}{12 - (-4)} = \frac{4}{16} = \frac{1}{4} \] Now that we have the slope \(m = \frac{1}{4}\), we can use the slope-intercept form of the equation, which is: \[ y = mx + b \] We need to find the y-intercept \(b\). We can use one of the points, for example \((-4, 2)\), and substitute \(x\), \(y\), and \(m\) into the equation to solve for \(b\): \[ 2 = \frac{1}{4}(-4) + b \] \[ 2 = -1 + b \] \[ b = 3 \] So, the y-intercept \(b\) is 3. Therefore, the equation of the line in slope-intercept form is: \[ y = \frac{1}{4}x + 3 \] This is the equation of the line passing through the points \((-4, 2)\) and \((12, 6)\).