Ask AI on The Internet
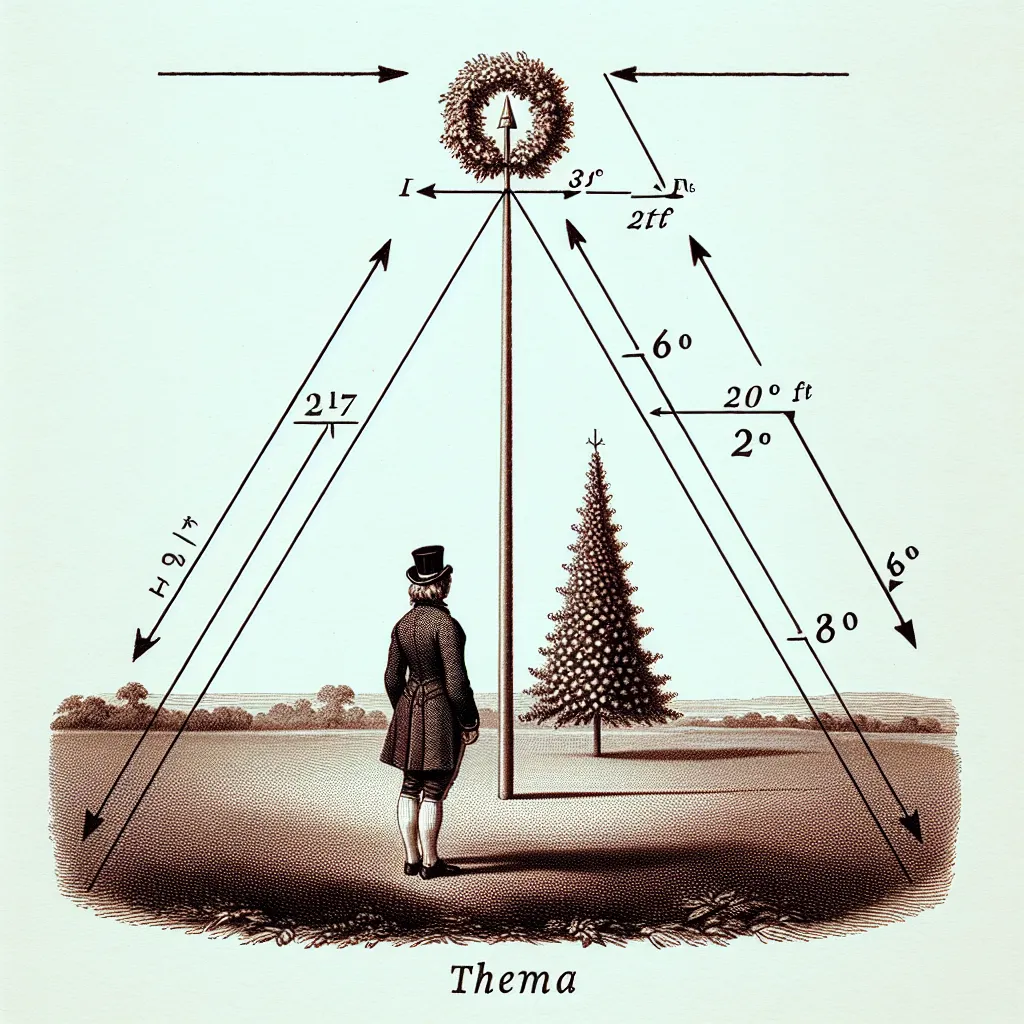
Question: Solve each application using right triangle trig. A fisherman is 129 meters from a lighthouse. If he looks up at the lighthouse at an angle of elevation of 36, how tall is the lighthouse?
To solve this problem, we will use trigonometric relationships in a right triangle. In this scenario, the fisherman forms a right triangle with the lighthouse where: - The horizontal distance from the fisherman to the lighthouse is one leg of the triangle. - The height of the lighthouse is the other leg of the triangle. - The angle of elevation from the fisherman to the top of the lighthouse is given. Let's summarize the given information: - Horizontal distance (adjacent side) = 129 meters - Angle of elevation = 36 degrees We need to find the height of the lighthouse (opposite side). We will use the tangent (tan) function in trigonometry, which relates the angle of a right triangle to the ratio of the opposite side to the adjacent side: \[ \tan(\text{angle}) = \frac{\text{opposite}}{\text{adjacent}} \] In this case: \[ \tan(36^\circ) = \frac{\text{height of the lighthouse}}{129 \text{ meters}} \] To find the height of the lighthouse, we rearrange the equation to solve for the opposite side (height): \[ \text{height of the lighthouse} = 129 \text{ meters} \times \tan(36^\circ) \] Now, we need to calculate the tangent of 36 degrees. You can use a scientific calculator for this: \[ \tan(36^\circ) \approx 0.7265 \] Substituting this value back into the equation: \[ \text{height of the lighthouse} = 129 \text{ meters} \times 0.7265 \] \[ \text{height of the lighthouse} \approx 93.71685 \text{ meters} \] Rounding to a reasonable precision: \[ \text{height of the lighthouse} \approx 93.72 \text{ meters} \] So, the height of the lighthouse is approximately 93.72 meters.
Think your answer is better than the AI's? Post it below.
Question Tags
If you want your question answered by an AI, click here.
![To find the height of the lighthouse, you can use the tangent function in right triangle trigonometry.
1. **Identify the triangle**: The fisherman, the base of the lighthouse, and the top of the lighthouse form a right triangle.
2. **Use the tangent function**: The formula for tangent in a right triangle is:
\[
\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}}
\]
where:
- \(\theta\) is the angle of elevation (36 degrees),
- the opposite side is the height of the light](https://theinternetioimages-f2htc2ggcrath6d7.z01.azurefd.net/$web/askai/d2a6c140-c40b-4140-955a-6fa8f26647b1.webp)




Post your own comment: